| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Android
- androidstudio
- bitmap
- BOJ
- Canvas
- CS
- Database
- DBeaver
- DP
- Ecilpse
- Eclipse
- firebase
- git
- github
- GooglePlayServices
- gradle
- IDE
- IntelliJ
- java
- json
- kotlin
- level2
- linux
- mariadb
- MYSQL
- Paint
- permission
- python
- Sorting
- sourcetree
will come true
[프로그래머스/Level2] 피보나치 수 본문
문제
https://programmers.co.kr/learn/courses/30/lessons/12945?language=java
코딩테스트 연습 - 피보나치 수
피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다. 예를들어 F(2) = F(0) + F(1) = 0 + 1 = 1 F(3) = F(1) + F(2) = 1 + 1 = 2 F(4) = F(2) + F(3) = 1 + 2 = 3 F(5) = F(3) + F(4) =
programmers.co.kr
풀이
피보나치 수
F(0) = 0, F(1) = 1 일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 성립하는 수
전형적인 DP문제 중 하나인 피보나치 수 구하기.
순서대로 나열된 항들이 일정한 규칙을 가지는 or 항들의 관계를 점화식으로 나타낼 수 있으면 DP문제.
재귀 함수를 사용하는 하향식(Top-Down) 방식, 반복문을 사용하는 상향식(Bottom-Up) 방식 중 하나를 선택하여 푼다.
구해야 할 피보나치 수가 F(3)일 때, TopDown방식과 BottomUp방식의 접근 순서 차이를 확인해보자.
Top-Down 방식 접근 순서
- F(3) = F(2) + F(1)
- F(2) = F(1) + F(0)
- F(1) = 1
- F(0) = 0
- F(1) = 1
- F(2) = F(1) + F(0)
- F(2) = 1 + 0
- F(3) = 1 + 1 = 2
Bottom-Up 방식 접근 순서
- F(0) = 0
- F(1) = 1
- F(2) = F(1) + F(0) = 0 + 1 = 1
- F(3) = F(2) + F(1) = 1 + 1 = 2
이렇게 두 가지 방식으로 DP문제를 풀 수 있지만, Top-Down 방식을 저대로만 하게되면 앞서 이미 구했던 피보나치 수들을 재귀 과정에서 또 다시 구하는 일이 발생하게 되어 Bottom-Up방식 보다 연산 횟수가 과하게 늘어나 시간초과에 걸리게 된다. Top-Down 방식도 추가적인 처리를 하면 타임아웃에 안 걸릴 거 같긴하지만.. 너무 번거로울 것 같기에Bottom-Up 방식으로 풀기로 했다.
코드
class Solution {
public int solution(int n) {
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i <= n; i++){
dp[i] = (dp[i-1] + dp[i-2]) % 1234567;
}
return dp[n] % 1234567;
}
}
- F(0) ~ F(n) 까지 피보나치 수를 저장할 dp배열 선언
- F(0)=0, F(1)=1 은 고정 값이기 때문에 미리 dp배열에 저장
- F(2) ~ F(n) 까지 순서대로 피보나치 수를 계산해 dp 배열에 저장
- 마지막으로 계산된 F(n) 값을 반환
아래와 같이 테스트 7~14에서 실패가 뜨는 경우는 F(0)~F(n) 까지의 피보나치수를 배열에 저장하는 for문에서 반복때마다 구해지는 새로운 피보나치수에 %1234567 연산을 수행하지 않았기 때문일 것이다.
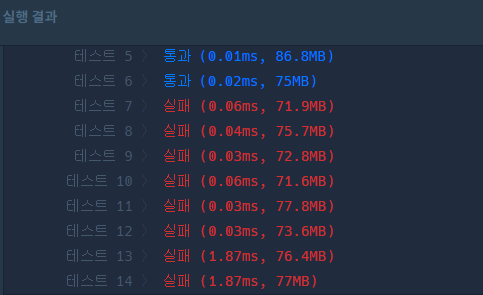
최종적으로 구해야하는 건 F(n) % 1234567 값이지만, F(n)을 구하기 까지 계산된 중간 피보나치 수들에 대해서도 똑같이 매번 %1234567 연산을 취해줘야 제대로 된 F(n) 값을 구할 수 있다. 위 연산을 빼먹으면 F(n)까지 오는 도중에 피보나치 수가 과하게 커져 int타입 표현 범위를 넘는 오버플로우가 발생해 값이 변조될 수 있다. 매 반복마다 %1234567을 해주면 F(n)까지의 모든 피보나치 수들은 절대 1234567값을 넘지 않는다.
dp[i] = (dp[i-1] + dp[i-2]) % 1234567;'Algorithm' 카테고리의 다른 글
| [프로그래머스/Level2] 숫자의 표현 (0) | 2022.01.14 |
|---|---|
| [프로그래머스/Level2] 최솟값 만들기 (0) | 2022.01.13 |
| [프로그래머스/Level2] JadenCase 문자열 만들기 (0) | 2022.01.12 |
| [프로그래머스/Level2] 행렬의 곱셈 (0) | 2022.01.12 |
| [프로그래머스/Level2] N개의 최소공배수 (Java) (0) | 2022.01.10 |

